Cet article est publié sous licence CC BY-NC-SA
Le travail de développeur c’est souvent un problème à modéliser puis à résoudre.
Les clients expriment leurs problèmes dans leur langue naturelle. Ils expriment de la même manière les solutions qu’ils imaginent. Les développeurs vont traduire tout ça dans un programme, dans une architecture, etc. Nous traduisons ainsi une abstraction en une autre.
Cette capacité de comprendre et de traduire les abstractions différencie chaque développeur. Tout n’est pas une question de capacité intrinsèque, rentre en jeu beaucoup d’autres facteurs comme : l’expérience, la méthodologie, les outils, etc.
Aujourd’hui je voudrais faire un tour des bases mathématiques utiles pour modéliser et résoudre. Selon notre parcours scolaire, on ne dispose pas tous des mêmes outils. Puisse ce petit survol (r)éveiller chez vous l’usage de l’arme mathématique.
Vous vous posez encore la question « Pourquoi les mathématiques sont-elles intéressantes pour un développeur ? ». Les mathématiques sont le pont entre le monde concret de la physique et le monde abstrait de l’informatique. Les processeurs sont basés sur la logique et l’arithmétique, les réseaux sur les graphes, etc. La programmation fonctionnelle est un bon exemple de l’influence des mathématiques sur l’informatique puisque même les langages que nous utilisons sont basés sur cette discipline.
Que ce soit lorsqu’on utilise les ensembles, les arbres, les machines à état ou lorsque l’on cherche à évaluer la complexité d’un algorithme, on utilise tous les mathématiques à notre insu. En maitrisant un peu mieux ces concepts, on est en mesure d’imaginer des solutions qui en tirent le meilleur.
Faute d’être capable de transmettre tous ces fondements je vais essayer d’en présenter trois deux et de lister les autres.
Avant de parler des relations, voilà quelques rappels sur les ensembles. Un ensemble \(A\) est souvent vu comme une collection d’objets. Tout objet, peut appartenir ou non à \(A\), lorsque c’est le cas, on appelle cet objet un élément de \(A\). On note respectivement \(x \in A\) et \(x \notin A\). On décrit souvent les ensembles par compréhension : \(A = \{ x \in \mathbb{N} \mid x \bmod 2 = 0 \}\) soit \(A\) l’ensemble des entiers naturels pairs. Pour définir les relations on utilisera le produit cartésien de \(E_1\) et \(E_2\) :
La notation par compréhension est largement utilisée dans les langages de programmation. Voici un exemple en Python :
# liste des 50 premiers entiers pairs
[x for x in range(100) if x % 2 == 0]
On va également avoir besoin par la suite des notions de sous ensemble, d’union, d’intersection et de différence qui sont assez naturelles mais que je rappel tout de même ici :
Les relations sont un des fondements de l’organisation de l’information en informatique. Tous les jours on utilise des relations comme \(\leq\), \(\geq\), \(=\), \(\neq\), etc. On appelle \(R\) une relation de \(A\) vers \(B\) un sous ensemble de \(A \times B\). Et on note \(x R y\) lorsque \((x, y) \in R\).
On note \(dom(R)\) le domaine d’une relation \(R\) sur \(A \times B\) tel que :
De la même manière \(img(R)\) est l’image d’une relation \(R\) sur \(A \times B\) tel que :
Exemple de relation
Les ensembles \(A\) et \(B\) peuvent contenir n’importe quel type d’objets. Par exemple, ((A\) peut contenir des utilisateurs et \(B\) des rôles. Une relation \(R\) entre ces deux ensembles pourra donc représenter les rôles des utilisateurs et on notera \(u R d\) pour dire que l’utilisateur u dispose du rôle r.
On peut représenter \(R = \{ (a,1), (a,2), (b,2), (d,4) \} \) par le diagramme suivant :
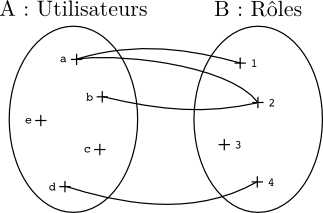
Pour \(R\) : \(dom(R) = \{a, b, d\}\) et \(img(R) = \{1, 2, 4\}\)
Exemples SQL
Ces notions d’ensembles, d’image et de domaine sont utilisés constamment en SQL. Reprenons notre exemple des utilisateurs, des rôles et de la relation \(R\). Pour encoder \(R\) en SQL, on utilise 3 tables, une table par ensemble et une table représentant la relation. En effet, on a vu que \(R \subseteq A \times B \) donc \(R\) est également un ensemble.
A B R
------ -------- -------------
| id | | name | | id | name |
------ -------- -------------
| a | | 1 | | a | 1 |
| b | | 2 | | a | 2 |
| c | | 3 | | b | 2 |
| d | | 4 | | d | 4 |
| e | -------- -------------
------
On va exprimer par un ensemble contenant des couples quelques requêtes SQL classiques.
SELECT * FROM R
SELECT A.id, B.name FROM A
INNER JOIN R
ON A.id = R.id
INNER JOIN B
ON B.name = R.name
-- => (a,1), (a,2), (b,2), (d,4)
SELECT A.id, B.name FROM A
LEFT JOIN R
ON A.id = R.id
LEFT JOIN B
ON B.name = R.name
-- => (a,1), (a,2), (b,2), (d,4), (c,null), (e,null)
SELECT A.id, B.name FROM A
RIGHT JOIN R
ON A.id = R.id
RIGHT JOIN B
ON B.name = R.name
-- => (a,1), (a,2), (b,2), (d,4), (null, 3)
SELECT A.id, B.name FROM A
FULL OUTER JOIN R
ON A.id = R.id
FULL OUTER JOIN B
ON B.name = R.name
-- => (a,1), (a,2), (b,2), (null, 3), (d,4), (c,null), (e,null)
SELECT A.id FROM A
LEFT JOIN R
ON A.id = R.id
WHERE R.id IS NULL
-- => (c), (e)
Composition de relations
Les relations étant de « simples » ensembles, les opérations ensemblistes qu’on a revues plus tôt s’y appliquent. Ce qui apparait par contre avec les relations c’est la notion de composition. Soit \(R_1 \subseteq A \times B\) et \(R_2 \subseteq B \times C\), on peut noter et définir la relations « \(R_2\) après \(R_1\) » :
Cette composition est également utilisée tous les jours dans le monde de la base de données. Si je reste sur mon exemple précédent, les ensembles \(A\), \(B\) et \(C\) représentent respectivement utilisateurs, rôles et produits. Je dispose toujours de \(R \subseteq A \times B\) mais admettons que je dispose maintenant de \(P \subseteq B \times C\) avec \(r P p\) signifiant qu’un rôle \(r\) peut accéder à un produit \(p\). La relation \(P \circ R\) me donne les produits disponibles pour un utilisateur donné.
Depuis le début de cette partie vous avez pu remarquer que le concept mathématique de relation permet d’exprimer de manière concise ce que nous manipulons quotidiennement. On peut presque imaginer réaliser des spécifications et des programmes entièrement formalisés de cette manière. En fait, ce n’est pas de l’imaginaire puisqu’il existe nombre de méthodes formelles comme la méthode B, le langage Esterel, et bien d’autres.
Propriétés des relations
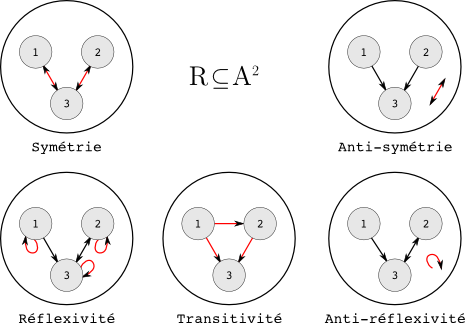
Les propriétés sur les relations sont un classique, on les a probablement tous vu au collège ou bien au lycée un jour ou l’autre. Donc voici un bref rappel de ces définitions. On utilisera une relation \(R\) telle que \(R \subseteq A^2\). Je ne l’ai pas encore précisé mais \(A^2 \equiv A \times A\) et des relations dans \(A^2\) peuvent être représentées par un graphe (si si, vous verrez).
Attention les « Anti-X » sont trompeuses, il ne s’agit pas de ne pas être X pour être Anti-X. Ces propriétés ne sont que du vocabulaire pour le moment, mais dès que nous allons parler des ordres, ce dernier nous sera utile. Ce n’est pas un glossaire exhaustif, je n’ai reporté que les propriétés les plus connues.
Depuis tout à l’heure je parle de base de données pour illustrer l’omniprésence des relations. Et, peut-être que certains lecteurs pensent que
je vais leur parler des fameux one_to_one, one_to_many et many_to_many si utilisés… Et bien ils ont tout juste !
On a vu que les relation se définissaient comme « un sous ensemble du produit cartésien de deux ensembles » : \(R \subseteq A \times B\).
Lorsque \(dom(R) = A\) on dit que la relation est totale, et, lorsque \(img(R) = B\) on dit que la relation est surjective.
Si nos utilisateurs ont obligatoirement un ou plusieurs rôles, alors \(R\) (la relation de mes précédents exemples) est totale.
Si tout les produits doivent avoir obligatoirement avoir un ou plusieurs rôles, alors \(P\) est surjective.
Donner une contrainte foreign_id NOT NULL c’est en fait « créer une relation surjective » !
Lorsque \(\forall x \in A, y \in A, z \in B : (x R z) \land (y R z) \implies x = y\) on dit que \(R\) est injective. De la même manière on peut avoir \(\forall x \in A, y \in B, z \in B : (x R y) \land (x R z) \implies y = z\), on dira alors de \(R\) qu’elle est fonctionnelle. Donc, si nos utilisateurs ne peuvent avoir qu’un seul et unique rôle, on dira que \(R\) est fonctionnelle. Et, si nos produits ne peuvent pas être partagés entres deux rôles, on dira que \(P\) est injective.
On vient de décrire respectivement many_to_one et one_to_many. Une relation injective et fonctionnelle sera donc une relation one_to_one.
Profitons de la situation pour définir une fonction au sens mathématique : c’est une relation fonctionnelle et totale, et c’est tout. On dit d’une relation qu’elle est bijective lorsqu’il s’agit d’une fonction qui est à la fois injective et surjective.
Cela fait beaucoup de vocabulaire, mais dites-vous déjà qu’il est commun à beaucoup de métiers quel que soit le pays. Et, dites-vous vous ensuite qu’il a un super schéma qui résume tout ça juste en dessous.
Avant de parler de récursivité, le concept qui nous intéresse en informatique, il faut réexpliquer ce qu’est la récurrence. La récurrence est un type de démonstration d’un prédicat \(p(n)\) qui se base sur :
En informatique on peut utiliser, entre autre, la récurrence pour démontrer qu’un morceau de code respecte une propriété.
Prenons l’exemple d’une fonction (plutôt mal écrite) fact(e) retournant \(e!\) :
def fact(e)
if n == 0
1
else
result = 1
for i in (1..e) do
result = result * i
end
result
end
end
On peut montrer \(p(e) := e ≥ 0 \vdash fact(e) ≥ e\). En langage naturel cela donne : « si e est supérieur ou égal à zéro alors fact(e) est supérieur ou égal à e ».
if, \(fact(0) = 1\) et donc \(fact(0) ≥ 0\)Il n’est pas toujours nécessaire de poser la démonstration pour savoir qu’une propriété est vérifiée. Cependant, avoir en tête les concepts de précondition (ici \(e ≥ 0\)), d’invariant de boucle et de terminaison permet d’avoir une meilleure confiance dans son code.
En informatique on va pouvoir définir des concepts de manière récursive. Un concept récursif fait mention de lui-même dans sa définition. La précédente fonction
fact s’écrit récursivement :
def fact(e)
e == 0 ? 1 : e * fact(e - 1)
end
Grâce à cette définition récursive on voit directement aussi bien le pas initial que le pas récurrent. Le pas récurrent s’exprime directement avec \(fact(e - 1)\) ce qui simplifie encore la démonstration. Certains langages permettent de définir encore plus clairement ces deux étapes, voici la définition du même concept en Erlang :
fact(1) -> 1;
fact(E) -> E * fact(E-1).
Si exprimer des concepts de manière récursive est souvent plus élégant et plus concis, beaucoup pensent qu’il est tout de même plus efficace d’éviter. Il existe plusieurs formes de récursivité. Notre exemple utilise une récursivité linéaire :
fact(3) = 3 * fact(2) fact(3) = 3 * (2 * fact(1)) fact(3) = 3 * (2 * (1 * fact(0))) fact(3) = 3 * (2 * (1 * 1)) fact(3) = 3 * (2 * 1) fact(3) = 3 * 2 fact(3) = 6
C’est à dire que plus la valeur de e sera élevée plus le nombre d’expansion sera élevé et cette augmentation est linéaire par rapport à e. Ainsi plus e est grand et plus l’évaluation sera couteuse en mémoire.
Il existe malheureusement des récursivités encore plus coûteuses.
Toujours en Erlang, voila une implémentation de la fonction fibo(n) qui donne le n-ième élément dans la suite de Fibonacci :
fibo(0) -> 0;
fibo(1) -> 1;
fibo(N) -> fibo(N-1) + fibo(N-2).
Regardons maintenant l’évaluation de fibo(5) :
fibo(5) = fibo(4) + fibo(3) fibo(5) = (fibo(3) + fibo(2)) + fibo(3) fibo(5) = ((fibo(2) + fibo(1)) + fibo(2)) + fibo(3) fibo(5) = (((fibo(1) + fibo(0)) + fibo(1)) + fibo(2)) + fibo(3) fibo(5) = (((1 + fibo(0)) + fibo(1)) + fibo(2)) + fibo(3) fibo(5) = (((1 + 0) + fibo(1)) + fibo(2)) + fibo(3) fibo(5) = ((1 + fibo(1)) + fibo(2)) + fibo(3) fibo(5) = ((1 + 1) + fibo(2)) + fibo(3) fibo(5) = (2 + fibo(2)) + fibo(3) fibo(5) = (2 + (fibo(1) + fibo(0))) + fibo(3) fibo(5) = (2 + (1 + fibo(0))) + fibo(3) fibo(5) = (2 + (1 + 0))) + fibo(3) fibo(5) = (2 + 1) + fibo(3) fibo(5) = 3 + fibo(3) fibo(5) = 3 + (fibo(2) + fibo(1)) fibo(5) = 3 + ((fibo(1) + fibo(0)) + fibo(1)) fibo(5) = 3 + ((1 + fibo(0)) + fibo(1)) fibo(5) = 3 + ((1 + 0) + fibo(1)) fibo(5) = 3 + (1 + fibo(1)) fibo(5) = 3 + (1 + 1) fibo(5) = 3 + 2 fibo(5) = 5
On constate que cette forme de récursivité est bien moins sympathique que la première. Dans la définition on fait deux fois mention de la fonction elle-même ce qui donne lieu à une récursivité sous forme d’arbre.
On peut écrire la fonction fact(n) de manière terminale :
fact(N) -> fact(N-1, N).
fact(1, N) -> N;
fact(I, N) -> fact(I-1, N * I).
Cela aura pour résultat une évaluation plus rapide :
fact(3) = fact(2, 3) fact(3) = fact(1, 3 * 2) fact(3) = fact(1, 6) fact(3) = 6
On a introduit un accumulateur chargé d’éviter l’expansion de fact.
Beaucoup de langage de programmation fournissent des itérateurs reprenant ce concept d’accumulateur. En Ruby on a par exemple reduce :
def fact(n)
n == 0 ? 1 : (1..n).reduce(1){|accu, i| accu * i}
end
La récurrence est beaucoup utilisée dans la preuve de programme, comme on l’a vu pour prouver des invariants de boucles mais pas uniquement. Jusque-là on a appliqué le concept de récursivité pour exprimer des suites sous forme de fonctions. On peut également exprimer un type de donnée grâce à ce concept.
Dans l’exemple suivant on va définir par récurrence une structure de donnée : List. Celui-ci est en Haskell.
data List a = Nil | Cons a (List a)
Cette structure représente une liste d’élément d’un même type a. Une liste peut être vide : Nil ou bien être un élément de type a suivi d’une autre liste : Cons a (List a).
Bien que l’exemple précédent représente une structure de donnée très simple, les types récursifs permettent de définir des concepts beaucoup plus complexes comme les graphes. Peu importe le langage utilisé, être à l’aise avec ce genre de structures et être capable d’en concevoir est une capacité indispensable au quotidien.
Une relation d’ordre est une relation sur un ensemble \(A\) qui dispose de certaines propriétés. Une relation d’ordre, comme \((\mathbb{N}, \leq)\), est : réflexive, transitive et anti-symétrique. Une relation d’ordre strict, comme \((\mathbb{N}, <)\), est : anti-réflexive, transitive et donc anti-symétrique.
Les ordres ainsi que les concepts qui gravitent autour sont indispensables en informatique. En effet, c’est grâce à eux que l’on peut « comparer » des informations. Les ordres permettent de trier l’information, d’y accéder de manière rapide, etc. Les ordres sont, eux aussi, partout.
Les graphes sont la représentation d’une relation symétrique. Les arrêtes entre les nœuds ne sont pas dirigées comme c’est le cas dans les schéma ci-dessus.
Les graphes sont de très bon supports pour modéliser des chemins, des réseaux, des hiérarchies (arbres), etc. Ils sont utilisés pour représenter des circuits, des automates, des réseaux (internet, sociaux, d’énergie, de distribution, routiers, téléphoniques, etc), des programmes informatiques, etc. Bref, les graphes sont des outils incontournables pour modéliser et résoudre.
Leur seul défaut, pour en parler dans un article il faut passer des heures et des heures sous Inkscape. Un défaut largement compensé par l’aspect ludique de leur apprentissage.
La logique c’est des notations, des concepts, des techniques et des outils mathématiques mais aussi informatiques permettant de montrer qu’un raisonnement, une déduction ou bien un programme est valide ou non.
La logique est un des piliers de l’informatique. La sémantique des langages, la démonstration, la complexité, l’intelligence artificielle, la vérification de programmes, et d’autres disciplines encore se reposent sur la logique. Si vous êtes désireux d’approcher un domaine théorique de l’informatique, vous ne pourrez pas sans de bonnes connaissances en logique. Sinon, c’est toujours utile dans la vie de tous les jours sans forcément que ce soit conscient ; au travers d’une meilleure compréhension du système de type qui n’infère pas ce qu’on veut ou encore d’une pseudo-démonstration sur un morceau de code problématique.
C’est terminé pour cette toute petite exploration des fondements mathématiques de l’informatique. J’aurai voulu être capable de vous en dire plus mais je me suis rendu compte que j’avais oublié bien des choses. Qui plus est l’article est déjà très long. J’espère que mon récit aura su vous faire voir que, sans nécessairement en être conscient, on fait des maths à longueur de temps. J’espère aussi que cela vous donnera envie d’en apprendre d’avantage.
Les mathématiques sont un langage commun à beaucoup de métiers, des non-informaticiens sont souvent capables de comprendre des énoncés au style « mathématique ».
Connaitre un peu mieux les fondements de concepts qu’on utilise tout les jours permet d’en assimiler de nouveaux plus facilement, d’être moins dépendant aux outils.
L’équipe Synbioz.
Libres d’être ensemble.
Nos conseils et ressources pour vos développements produit.